A
Modular Percussion Synthesis Environment
The fun thing about physical modelling synthesis (and maybe the very point of it all) is to create your own instruments, out of basic components, or modules. Modular synthesis, as it is known, is not a new idea---it goes back to the earliest days of physical modelling, and is the basic strategy behind the CORDIS environment. The idea here is rather different from that of pure musical acoustics, in that one is building an instrument without a real-world counterpart---but which still obeys the laws of physics.
Percussion is a good candidate for a modular
system---control is fairly simple, compared with other instrument types, and it
is difficult to come up with a modular construction which does not produce
sound. Below is a brief description of a modular synthesis environment, based
on finite difference schemes, and presented recently at the 2009 Digital Audio Effects Conference
in
The basic building blocks in a percussion synthesis environment are bars and flat rectangular plates---here, these will be assumed to be of uniform cross-section/thickness, and linear.


One could go a lot further here, and explore more realistic features, such as variations in thickness or geometry, plate curvature, nonlinearities, etc., but the above suffices for a simple percussion network---and the range of sounds it is possible to produce is very large indeed, more than enough to satisfy an inquisitive composer/instrument designer! If you really want to know more about these more subtle features, see the text.
In order to form a network, connections are necessary. These behave as springs (possibly nonlinear) or dampers, or a combination of both, and are also characterized by spatial distributions, indicating how exactly they are affixed to the objects, of bar or plate type. One can specify as many connections as desired, which can overlap one-another.
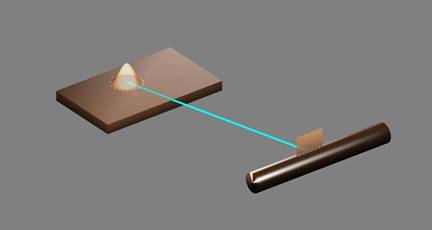
Playing the instrument is effected by sending force-like pulses (also characterized by spatial distributions, perhaps to mimic the finite regon of contact of a mallet with a real instrument) to the instrument at specified times and of specified durations. A typical excitation in a real percussion instrument is on the order of between 1 and 5 milliseconds. Once an instrument is built, the user must then specify a score, consisting of a list of these events.
The systems can be discretized by standard finite difference methods:

Here is a short video clip of the behaviour of illustrating the behaviour of a very simple network, consisting of three plates, four bars and seven connections:
Just as an illustration of the basic properties of the elements in these networks, consider the case of a set of uncoupled bars, as below:

Here is a basic percussive gesture:
In this simple setting, it’s easy to hear the effects of varying the boundary conditions of the bar, leading to changes in tuning…
…or damping rates…
…and striking positions…
Consider, now, a collection
of bars connected by nonlinear springs…this is best thought of as a form
of “preparation,” along the lines of the prepared piano…
The sounds are now of a completely different character…the nonlinear behaviour of the springs means that the sound output is highly dependent on the strength of the input, which is very much in line with true percussion instruments…here are a couple of sound examples

It is also possible to use plates as resonating
elements…

…and also to use the plates, on their own, as primary
struck elements, leading to percussive sounds more like those of cymbals and
drums…
Recently, a short
piece was composed by Gordon Delap, at the