
Laser Light Crystallography

 | Laser Light Crystallography |  |
The graphs below show typical laser light crystallography traces obtained for the various binary crystals. Information by each trace shows what crystal structure is described and the make up of the pair of particles used to make it. How to calculate size and volume fraction of the unit cell is also described.
For a cubic lattice the distance between Bragg planes, d, is related to a, the edge length via,
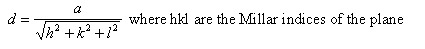 |
It is also possible to relate the scattering vector, Q, to d via the expression Qd=2p . If this is substituted into the above equation then we get
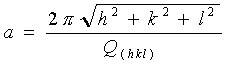 |
If the peaks within the laser light scattering trace can be asigned their correct (hkl) value then the Q vector for which they occur can now be used to calculate the crystal's lattice parameters and from these the volume fraction of the crystal can be determined i.e. total volume of spheres within unit cell/unit cell volume.
For sample phase diagram and SEM photographs of this structure follow the links
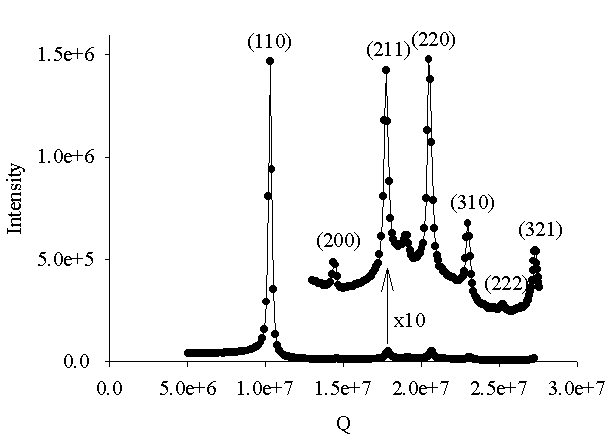 | The BCC crystallography trace seen for a size ratio of 0.400 containing particles with radii of 324.7nm and 130nm. |
For sample phase diagram of this structure follow the links
 | The crystallography trace seen for the cubic AB6 binary crystal seen at a size ratio of 0.399 |
For sample phase diagram and SEM photographs of this structure follow the links
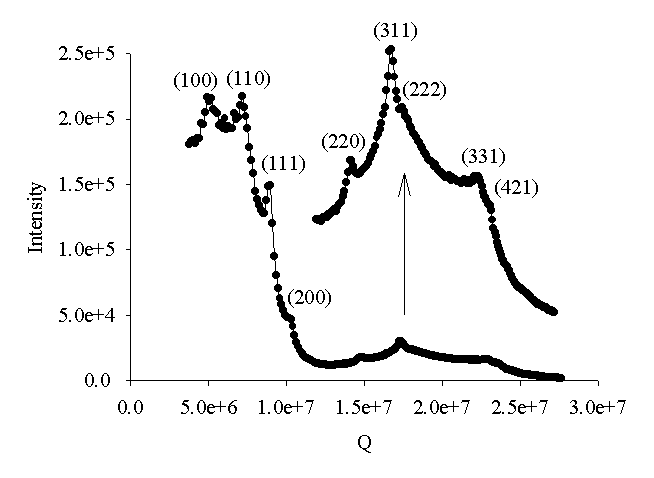
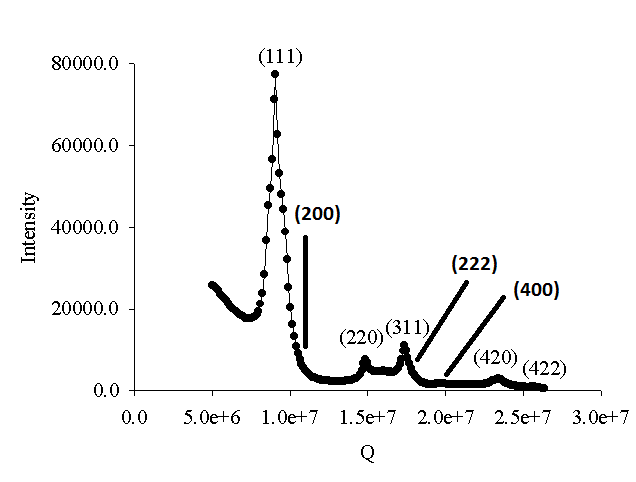 | The crystallography trace seen for the face-centred-cubic AB binary crystal at a size ratio of 0.399. Note the broadening in the (111) peak which indicates stacking faults between the large particle layers. |
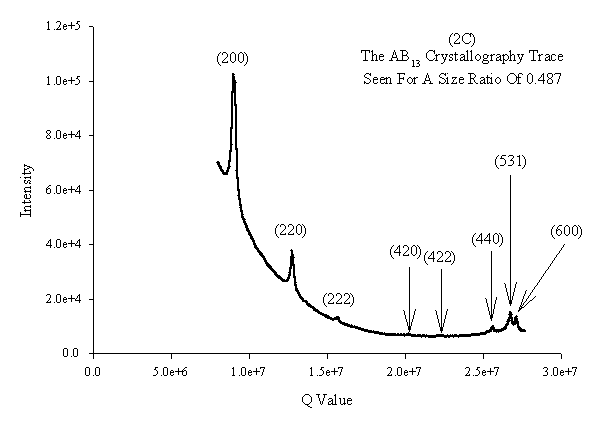 | The crystallography trace seen for the AB13 superlattice binary crystal seen at a size ratio of 0.486. This is the lowest size ratio at which this structure has been seen. From the position of the (200) peak the cubic a lattice parameter was determined as 1383nm giving the AB13 crystal a volume fraction of 0.6029. |
For sample phase diagram and SEM images follow the links
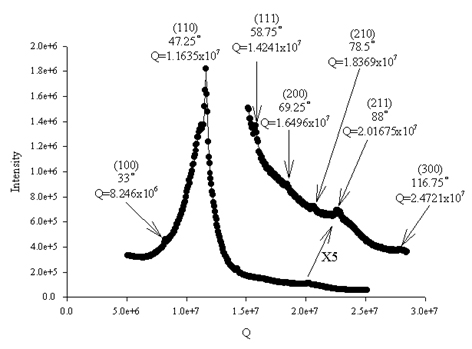 | The crystallography trace seen for the CsCl binary crystal seen at a size ratio of 0.736. This is the only size ratio at which this structure has been seen. |
For a known hexagonal lattice;
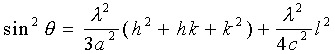 | where hkl are the Millar indices and a and c are the lattice parameters |
Substituting from Q=(4p/l)sin(q) for sin2q we get;

Assuming the largest lattice parameter, and hence smallest Q, is the (001) peak we can obtain a value for C and that the next peak is due to the (100) plane we can get A. These give us the lattice edge lengths a and c and allows us to assign (hkl) values for the other peaks. By simply geometry it can be shown that the volume of a hexagonal unit cell is;
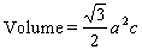
For sample phase diagram of this structure follow the links
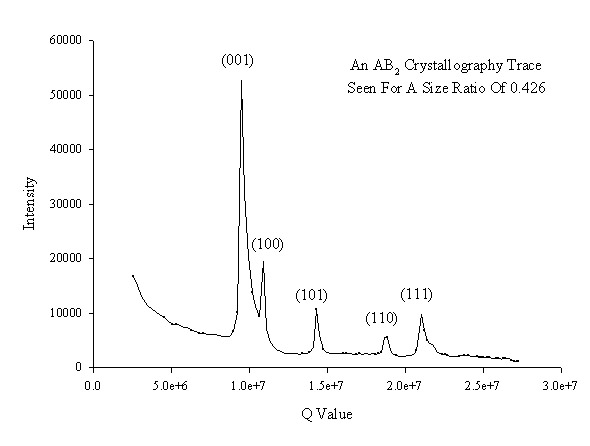 | This crystallography trace for an AB2 binary crystal is obtained from a sample made up of particles with radii of 324.7nm and 138.5nm giving the system a size ratio of 0.4265. This is the lowest size ratio at which this type of binary structure has been seen. From the peak positions the a lattice parameter was determined as 667nm and the c lattice parameter as 664nm giving the entire crystal a volume fraction of 0.6475. |